그동안 공부만 하고 포스팅을 미루었었는데, 오늘은 그간 공부한 내용 중 핵심적인 내용인 계절성 ARIMA 모델, SARIMA 모델에 대해 간단하게 정리해보겠다.
계절성 ARIMA 모델, SARIMA
앞서 데이터의 정상성을 설명할 때, 추세나 계절성을 없애고 싶으면 차분을 진행하고, 분산을 일정하게 만들고 싶으면 로그를 씌운다고 공부한 바가 있다. 그래서 데이터의 계절성을 제거하고 싶을 때 1차 차분 내지 2차 차분을 진행했다. 하지만 SARIMA 에선, 데이터의 계절성을 차분을 통해 진행하는 것이 아닌 그대로 안고 간다고 생각하면 될 것이다. 자세한 건 밑의 예시에서 다루기로 하고, 필요한 개념들을 빠르게 훑어보자.
계절성 차분
앞서 공부한 1차 차분은, 현재 데이터와 이전 데이터, 즉 시차가 1인 데이터끼리 뺀 것이었다. 2차 차분은 1차 차분한 데이터에서 다시 1차 차분을 진행하면 2차 차분이 되었다.
그에 반해 계절성 차분은,

이렇게 시차가 m 인 데이터들끼리 차분을 진행한다. 여기서 m 은? 당연히 계절성이 나타나는 주기가 될 것이다. 계절성이라는 개념은 꼭 계절마다 나타나야 하는 것이 아니고, 1주일마다, 1달마다 나타날 수도 있는 것이다. 만약 1주일마다 계절성이 보인다면 m = 7 이 될 것이다. 어렵지 않은 내용이지만, SARIMA를 설명하려면 이렇게 계절성 차분이라는 것이 존재함을 알고 있어야 할 것 같다.
SARIMA 에서 계수 선택
ARIMA 모델에서 사용한 계수는 (p, d, q) 총 3개였다. 원래 데이터의 AR 모델과 MA 모델을 해석하고, 차분 진행 정도를 계수로 선택했는데, SAIRIMA 모델에서는 계수가 4개가 증가한다. 이를 일반적으로 (P, D, Q, m) 이라 칭한다. 즉, SARIMA 모델은 데이터의 비계절성 부분을 (p, d, q) 로 설명하고, 계절성 부분을 (P, D, Q, m) 으로 설명한다는 것이다. m은 위의 계절성 차분을 설명했을 때의 m과 똑같다.
그렇다면 나머지 계절성 부분의 계수, PDQ는 어떻게 선택할까?
ARIMA 모델에서 계수를 선택할 때와 비슷하다.
| ACF | PACF | |
| AR(p) | 그래프가 서서히 감소 or 사인 함수 모양 | 그래프가 p lag 이후로 절단 |
| MA(q) | 그래프가 q lag 이후로 절단 | 그래프가 서서히 감소 or 사인 함수 모양 |
이게 ARIMA 모델에서 p 와 q를 선택하는 방법이었다. SARIMA 모델에서 계절성 부분의 계수 선택법은 다음과 같다.
| ACF | PACF | |
| AR(1) | 그래프가 서서히 감소 or 사인 함수 모양 | 그래프가 m의 배수의 시차들에서 유의미하게 증가 |
| MA(1) | 그래프가 m의 배수의 시차들에서 유의미하게 증가 | 그래프가 서서히 감소 or 사인 함수 모양 |
계절성 부분의 차분 계수 D는 비계절성에서처럼 차분을 진행한 횟수같은 의미이다. 단, 앞서 설명한 계절성 차분을 실행한 횟수이다. 보통 0 아니면 1을 갖는다고 하는데, 내 생각엔 계절성을 띄는게 확실하다면 알맞은 주기 m을 설정한 뒤 D를 1로 설정하는 것이 맞는 것 같다.
P와 Q의 선택에 있어서 특이한 점은 1 아니면 0 만을 갖는다는 점이다. 따라서 P+Q의 값은 2를 넘을 수가 없다. 즉 가능한 P와 Q의 순서쌍은 (0 , 0), (0 , 1), (1 , 0) 이렇게 3개밖에 될 수 없다. ARIMA 모델과 다른 점이다.
ARIMA 모델의 원리와 비슷하여 추가적으로 설명할 내용은 없을 것 같다. 이제 실전으로 넘어가보자.
SARIMA 파이썬으로 사용해보기
괜찮은 데이터셋을 구하는데에 실패해서, 파이썬의 statsmodels 패키지에 있는 연간 이산화탄소 배출량 데이터를 사용하기로 했다. 뚜렷한 계절성을 띄고 있어서 분석하기가 좋았다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
# Load the data into a Pandas DataFrame
data = sm.datasets.co2.load_pandas()
df = data.data
# Convert the data to a time series format
ts = df['co2'].resample('M').mean()
print(ts)
ts=ts.dropna()
print(ts)
# Plot the time series data
plt.plot(ts)
plt.xlabel("Year")
plt.ylabel("CO2 Concentration (ppm)")
plt.title("Monthly Mean CO2 Concentration")
plt.show()
# Plot the ACF and PACF of the time series data
sm.graphics.tsa.plot_acf(ts)
plt.show()
sm.graphics.tsa.plot_pacf(ts)
plt.show()
|
cs |



본 데이터를 월평균으로 합쳐서 데이터프레임을 구성했다. 1년에 1번씩 이산화탄소 배출량이 확 증가하는 것을 확인할 수 있는데, 이유는 잘 모르겠다. 아무튼 계절성 차수 m 은 12로 설정하기로 했다.
그 다음은 ACF 와 PACF 를 확인해보자. ACF 가 서서히 감소하는 모양, PACF 가 lag 12 에서 뚝 떨어지는 모습을 보이므로 계절성 부분의 차수는 (1, 1, 0, 12) 가 될 것이다.
이제 ARIMA 모델처럼 test set 과 train set 으로 데이터를 분리한 뒤 SARIMA 모델을 돌려보겠다. statsmodels 패키지에 SARIMAX 함수가 있어서 이를 사용했다. 위에서 데이터를 전처리했었는데 다시 데이터를 로드한 이유는 마지막에 설명하고 넘어가겠다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.statespace.sarimax import SARIMAX
# Load the data into a Pandas DataFrame
data = sm.datasets.co2.load_pandas()
df = data.data
df=df.dropna(subset=['co2'])
# Convert the data to a time series format
ts = df['co2'].resample('M').mean()
# Split the data into training and testing sets
train = ts[:-12]
test = ts[-12:]
# Fit the SARIMA model to the training data
model = SARIMAX(train, order=(1,1,1), seasonal_order=(1,1,0,12))
results = model.fit()
# Use the SARIMA model to make predictions for the testing data
predictions = results.predict(start=test.index[0], end=test.index[-1], dynamic=False)
# Plot the actual and predicted values for the testing data
plt.plot(train, label="Training Data")
plt.plot(test, label="Actual Values",linewidth='3')
plt.plot(predictions, label="Predicted Values")
plt.xlabel("Year")
plt.ylabel("CO2 Concentration (ppm)")
plt.title("SARIMA Model")
plt.legend()
plt.show()
|
cs |

ARIMA 모델로 예측했을 때는 예측모델이 직선으로 나오고 이래서 성능이 좋지 않은 모습을 보였는데, 얼핏 봐도 SARIMA 모델은 예측이 아주 잘 된 것으로 보인다. SARIMA 모델의 잔차를 분석함으로써 성능까지 테스트해보았다.
SARIMAX Results
===========================================================================================
Dep. Variable: co2 No. Observations: 514
Model: SARIMAX(1, 1, 1)x(1, 1, [], 12) Log Likelihood -195.158
Date: Wed, 08 Feb 2023 AIC 398.317
Time: 20:34:26 BIC 415.183
Sample: 03-31-1958 HQIC 404.935
- 12-31-2000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.1399 0.120 1.170 0.242 -0.094 0.374
ma.L1 -0.4959 0.106 -4.684 0.000 -0.703 -0.288
ar.S.L12 -0.4455 0.039 -11.342 0.000 -0.522 -0.369
sigma2 0.1197 0.008 15.453 0.000 0.105 0.135
===================================================================================
Ljung-Box (L1) (Q): 0.03 Jarque-Bera (JB): 0.01
Prob(Q): 0.85 Prob(JB): 0.99
Heteroskedasticity (H): 0.79 Skew: 0.01
Prob(H) (two-sided): 0.13 Kurtosis: 3.00
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).SARIMA 모델의 summary 함수를 사용해서 결과를 우선 보았다. Ljung-Box 값이 0에 가깝고 Prob(Q) 값이 1에 가까우므로 에측 성능이 좋음을 알 수 있다.

다음은 resid 함수를 이용해 잔차를 확인해보았다. 거의 0에 가까운 값을 보여주고 있음을 확인할 수 있다.
|
1
2
|
model.fit().plot_diagnostics(figsize = (16,9))
plt.show()
|
cs |
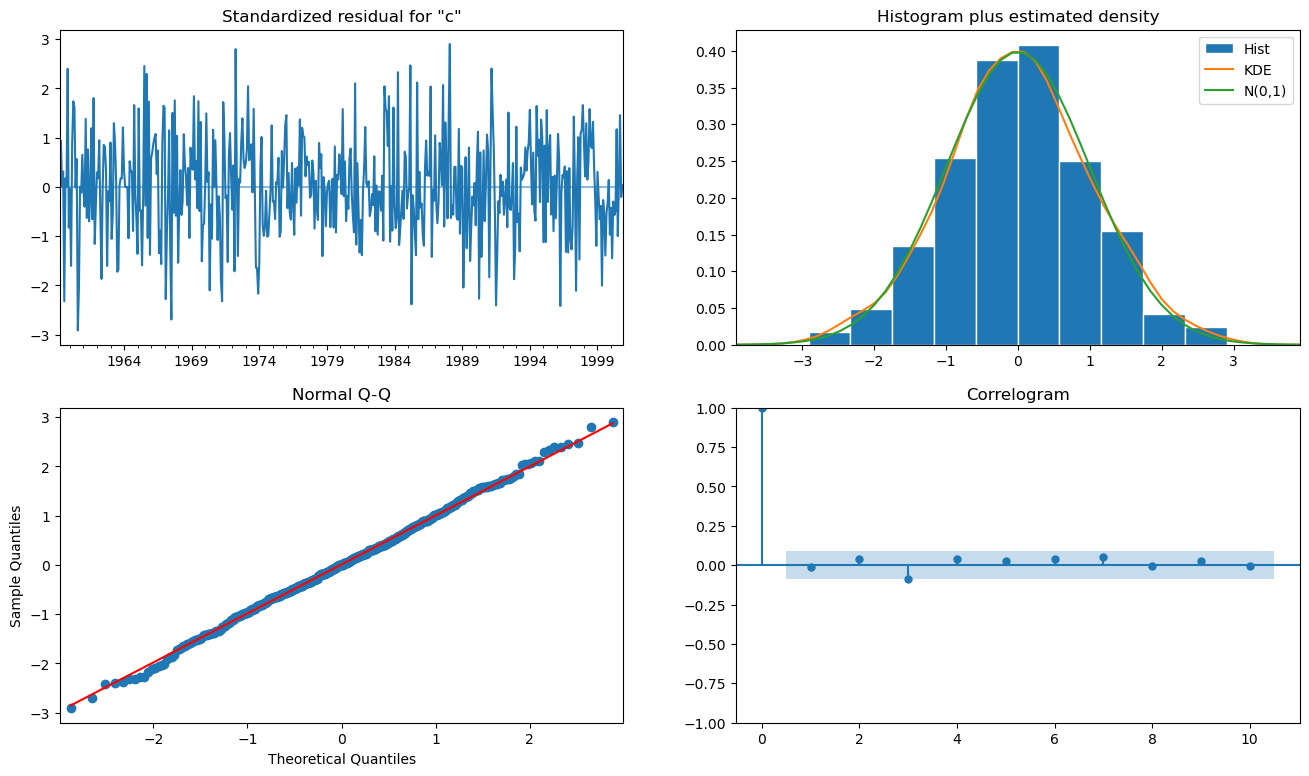
마지막으로 최근에 공부하면서 배운 plot_diagnostics 함수를 이용해서도 잔차를 확인해보았다. 사실 이 함수 하나면 위의 잔차 확인 작업은 필요가 없어지는 느낌이 있다. 그래서 앞으로 공부할 때는 plot_diagnostics 함수만 사용할 것 같다. 아무튼 결과를 확인해보니 잔차도 0에 가깝고, 정규분포에 가까움을 알 수 있었다.
SARIMA 함수로 좋은 결과를 얻었으나, 데이터가 좋았기 때문에 SARIMA 모델이 ARIMA 모델보다 좋다! 라고 단언할 수는 없을 것 같다.
마지막으로 SARIMA 모델을 쓰면서 데이터 처리를 다시 해준 이유를 작성하려고 했는데, 글이 너무 길어진 관계로 새로 포스팅을 한 번 더 하도록 하며 글을 마치겠다.
'시계열 데이터' 카테고리의 다른 글
| 시계열 데이터 - 코로나 확진자 수 ARIMA 모델로 예측하기 (2) (0) | 2023.02.10 |
|---|---|
| 시계열 데이터 - 코로나19 확진자 수 ARIMA 모델로 예측하기 (1) (0) | 2023.02.08 |
| 시계열 데이터 - AR,MA,ARIMA 모델 (2) | 2023.01.21 |
| 시계열 데이터 - 자기상관함수 ACF와 PACF (2) | 2023.01.15 |
| 시계열 데이터 분석 이론 정리 - 정상성과 비정상성 (0) | 2023.01.09 |



