저번 포스팅에 이어 코로나 확진자 수를 ARIMA 모델을 사용해 예측해본 결과를 마저 기록해보도록 하겠다.
https://tiabet0929.tistory.com/10
시계열 데이터 - 코로나19 확진자 수 ARIMA 모델로 예측하기 (1)
스터디에서 데이콘의 코드를 참고하여 그동안 공부한 내용들을 사용해 실제 데이터에 적용해보는 시간을 가졌었다. 스터디에서 참고한 코드는 아래의 두 편이다. "차트만으로 코스피를 예측할
tiabet0929.tistory.com
https://github.com/Tiabet/Time-series/blob/master/Time-series/Covid-19%20weekly.ipynb
GitHub - Tiabet/Time-series
Contribute to Tiabet/Time-series development by creating an account on GitHub.
github.com
사용한 데이터
사용한 데이터는 1편에서와 같은데, 다만 1주일치를 다 합해주는 작업을 진행했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
import pandas as pd
from statsmodels.tsa.ar_model import AutoReg
import matplotlib.pyplot as plt
# Load the data
df = pd.read_excel("Covid19.xlsx")
# Convert the date column to a datetime type
df['Date'] = pd.to_datetime(df['Date'])
# Set the date column as the index
df = df.set_index('Date')
# Resample the daily data to get the weekly sum of cases
df_weekly = df.resample('W').sum()
df_weekly = df_weekly.rename(columns={'Daily': 'Weekly'})
df_weekly = df_weekly[['Weekly']]
|
cs |
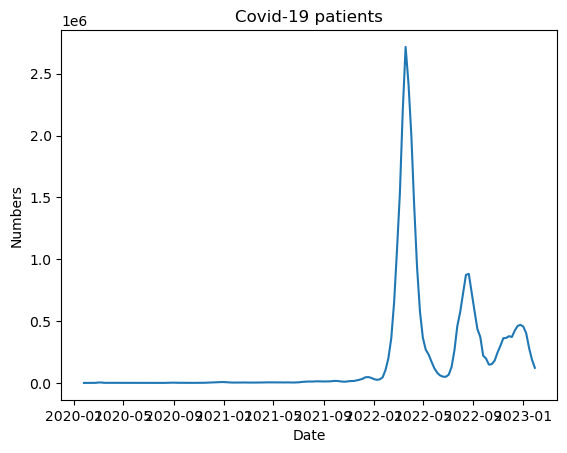
역시나 초반부에 0에 가까운 데이터들이 너무 많기 때문에 좋은 결과가 나오지 않을 것 같았다.
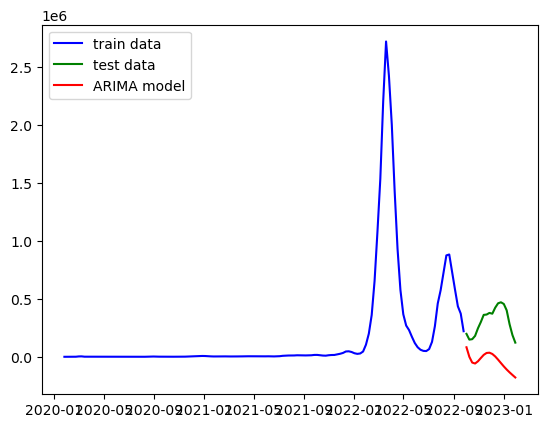
그리고 역시나 초반 데이터들 때문에 음수로 예측해버리는 결과가 나오고 말았다. (실행 코드는 1편에서와 같아서 생략)
그래서 이번에도 마지막 1년치의 데이터만 사용해보기로 했다.
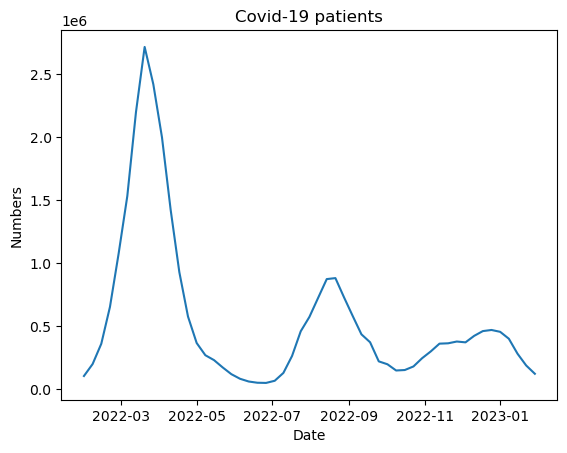
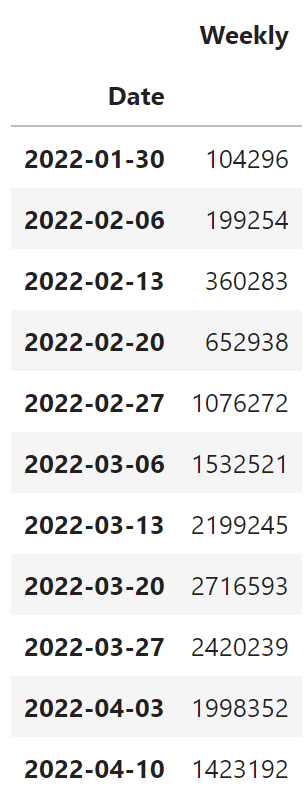
예측 진행
|
1
2
3
4
5
6
7
8
9
10
|
from sklearn.model_selection import train_test_split
train_size = 45
train_data, test_data = train_test_split(df_weekly, train_size=train_size, shuffle=False)
test_data = test_data.Weekly
train_data = train_data.Weekly
train_data
|
cs |
이번엔 싸이킷런의 train_test_split 함수를 이용해 test set 과 train set 으로 데이터를 분리해서 사용하기로 했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
from statsmodels.tsa.arima.model import ARIMA
import warnings
import itertools
warnings.filterwarnings("ignore") # to suppress warnings
p = d = q = range(0, 5) # parameter combinations for ARIMA model
pdq = list(itertools.product(p, d, q))
best_AIC = float("inf") # Initialize the best AIC score as infinity
best_params = None # Initialize the best parameters as None
for param in pdq:
try:
model = ARIMA(train_data, order=param)
res = model.fit()
if res.aic < best_AIC:
best_AIC = res.aic
best_params = (param)
except:
continue
print("Best ARIMA parameters: ", best_params)
|
cs |
역시나 자동으로 최적의 계수를 찾아주는 코드를 재활용했다. ACF, PACF 보고 찾아도 되는데 솔직히 이게 더 편하고 정확하니까..
Best ARIMA parameters: (1, 4, 2)아무튼 나온 최적의 계수는 (1, 4, 2) 가 나왔다. 의외인 점은 내가 공부한 바로는 차분은 2 이상 하지 않는 것이 좋다고 배웠는데, 아무래도 예외는 늘 있는 법인 것 같다. (1편에선 차분이 다 1이었음)
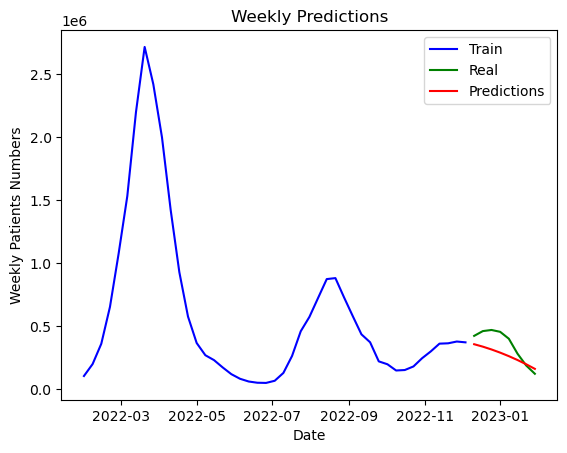
오.. 그나마 모양새는 비슷하게 예측했다.
|
1
2
3
4
5
6
7
8
9
10
11
|
# Generate predictions and calculate confidence interval
pred = model_fit.get_prediction(start=test_data.index[0], end=test_data.index[-1], dynamic=False)
pred_conf = pred.conf_int()
# Plot predictions and fill between the upper and lower bounds of the confidence interval
plt.plot(test_data, label='Observed')
plt.plot(pred.predicted_mean, 'r', label='Predicted')
plt.fill_between(pred_conf.index, pred_conf.iloc[:,0], pred_conf.iloc[:,1], color='gray',alpha=0.2)
plt.ylim(0,1000000)
plt.legend()
plt.show()
|
cs |
이번엔 예측의 신뢰구간 안에 ARIMA 모델이 들어오는지 확인해보고 싶어서 코드를 짜봤다.
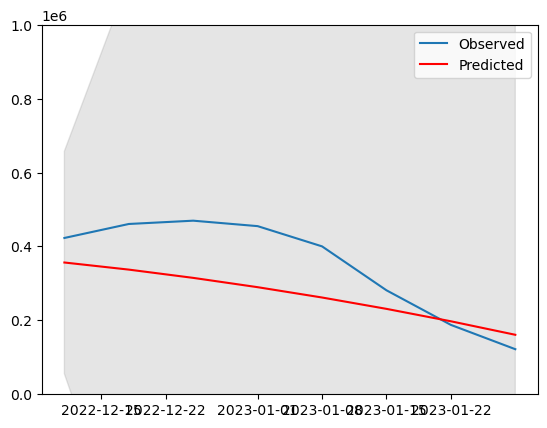
회색 영역이 신뢰구간인데, 무난하게 안정적으로 들어왔음을 확인할 수 있었다.
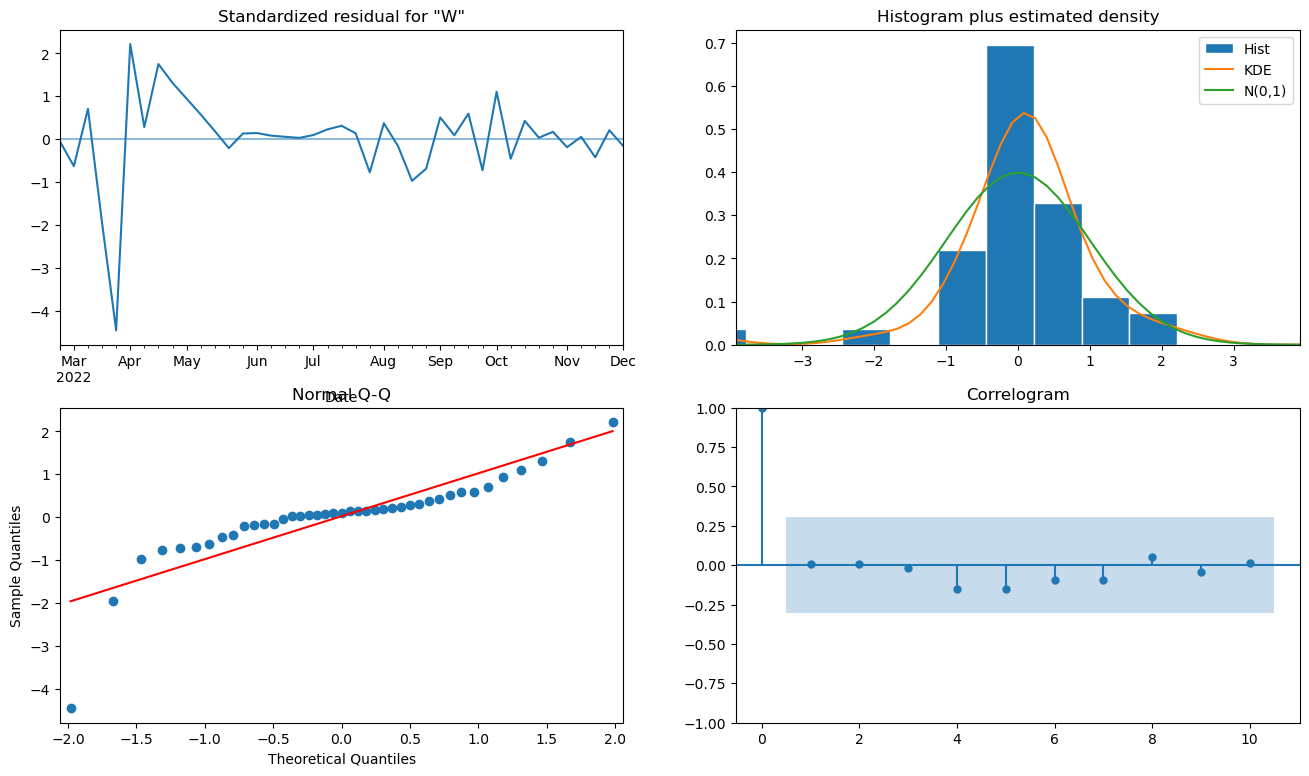
plot_diagnotics 함수의 결과를 보더라도 1편에서보다 괜찮아보이는 것 같다. 물론 초반부의 저 큰 잔차는 어쩔 수 없는 것 같지만..
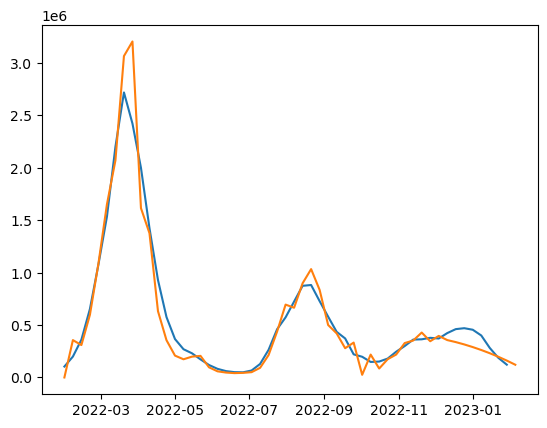
이건 전체 모델의 결과이다.
2023-02-05 121397.499961
Freq: W-SUN, dtype: float641월 30일부터 2월 5일까지의 확진자 수를 121397명으로 예측했었다. (이 코드를 돌린 것은 2월 3일 경이었고, 데이터가 1월 30일까지 존재했다.) 실제 같은 구간 확진자수는 10만 5천명 정도로, 예상치보다 1만 5천명 정도 적었다. 오차율로 치면 대략 10퍼센트 정도 되는 것 같다.
다음은 Seaborn 패키지의 함수 두 개를 사용해보았다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
import seaborn as sns
import matplotlib.pyplot as plt
prediction_total = model_fit.predict(start=0, end=len(weekly)-1, typ='levels')
# Combine the actual values and the predicted values into a single dataframe
df_predict = pd.DataFrame({'Actual': weekly, 'Predicted': prediction_total})
# Plot the actual and predicted values using the lineplot function
sns.lineplot(data=df_predict)
# Add labels and title to the plot
plt.xlabel('Time (days)')
plt.ylabel('Number of Covid-19 Patients')
plt.title('Actual vs Predicted Covid-19 Patients')
# Show the plot
plt.show()
# Regplot
sns.regplot(x='Actual', y='Predicted', data=df_predict)
plt.show()
|
cs |
Seaborn 패키지도 Matpltolib과 함게 파이썬의 기본적인 시각화 패키지인데, 이번 기회에 한 번 써보았다.
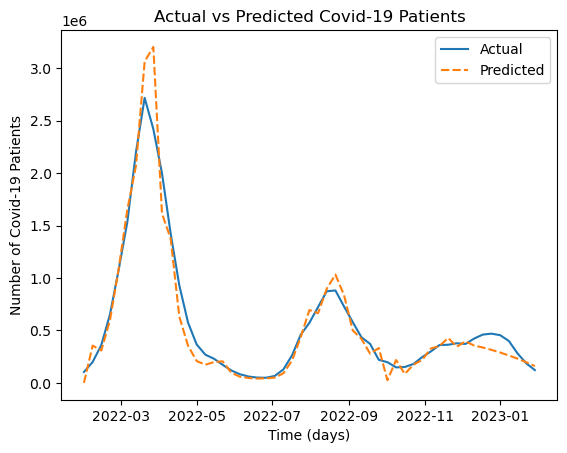
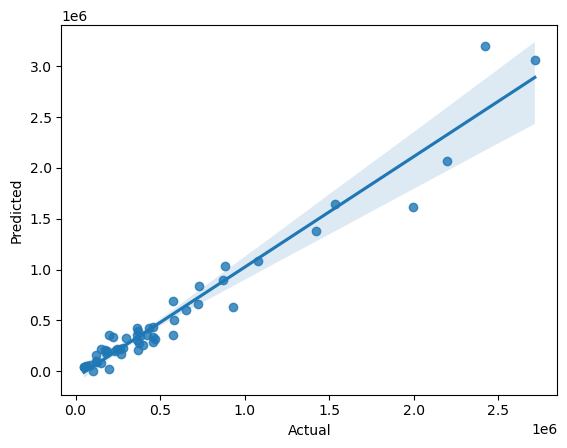
다음은 로지스틱회귀분석 코드를 짜봐서 진행해보았다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix
# Get the values for the target variable, which is whether the number of confirmed cases tomorrow is more than today
target = (weekly.diff() > 0).astype(int)
# Remove the first row from the data, as there is no previous day to compare the first day's confirmed cases to
data = weekly.iloc[1:]
target = target.iloc[1:]
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=42)
#Reshaping for 2D array
X_train = np.array(X_train)
y_train = np.array(y_train)
X_test = np.array(X_test)
y_test = np.array(y_test)
X_train = X_train.reshape(-1, 1)
y_train = y_train.reshape(-1,1)
X_test= X_test.reshape(-1, 1)
y_test = y_test.reshape(-1, 1)
# Train the Logistic Regression model on the training data
model = LogisticRegression()
model.fit(X_train, y_train)
# Use the trained model to make predictions on the test data
y_pred = model.predict(X_test)
# Evaluate the model's performance using accuracy score and confusion matrix
print("Accuracy score:", accuracy_score(y_test, y_pred))
print("Confusion matrix:\n", confusion_matrix(y_test, y_pred))
plt.title("Confusion Matrix of Patients Prediction")
sns.heatmap(confusion_matrix(y_test, y_pred,normalize="pred",), annot=True)
|
cs |
ChatGPT의 도움을 많이 받았다.
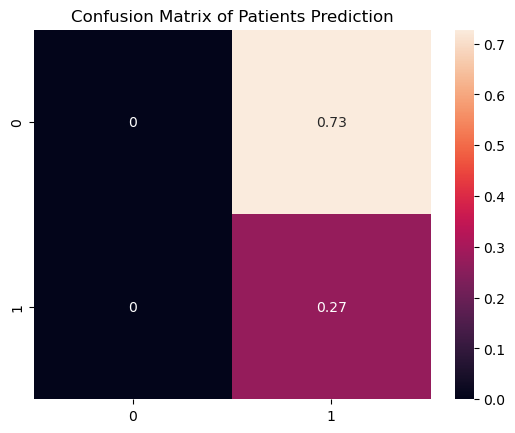
로지스틱회귀분석을 잘 알지는 못하는데, 사건이 발생할 것인지 아닐지를 예측할 수 있게 해준다고 한다. Confusion Matrix는 그 결과를 보기 쉽게 시각화해준 것인데, 왼쪽 위부터 Positive-True, Positive-False, Negative-True, Negative-False 라고 이해하면 된다. 즉 대각선에 위치한 숫자가 맞게 예측한 퍼센트라고 보면 된다. 적중률이 27퍼센트 정도로 매우 낮음을 확인할 수 있었다. 사실 함수를 정확히 쓸 줄 몰라서 Positive 항목은 제대로 사용해보질 못 했다. 이는 나중에 로지스틱 회귀분석을 제대로 공부하면 다시 사용할 기회가 있을 것 같다.
분석 결론
사실 이렇게 단순히 확진자를 예측하는 것이 빅데이터를 정말 유용하게 사용한다고 보긴 힘들다. 거리두기 같은 특정 제도를 실행했을 때 감염병 예방 효과가 얼마나 뛰어날지, 백신을 맞췄을 때와 맞추지 않았을 때 확진자 수가 얼마나 차이가 날지, 이런 걸 파악하고 예측할 수 있어야 빅데이터가, 또 빅데이터 분석이 빛을 발한다고 생각한다. 물론 이런 경지까지 올라가려면 많은 시간이 걸리겠고 또 공부할 것도 엄청 많겠지만.. 그래서 분석을 진행해보면서 다시 한 번 공부할 게 정말 많다는 사실을 배울 수 있었다.
다음 포스팅은 auto_arima 함수를 써서 어떤 데이터가 들어오더라도 분석 결과를 내놓는 그런 코드를 짜봤었는데, 그 결과를 공유해보도록 하겠다.
'시계열 데이터' 카테고리의 다른 글
| 시계열 데이터 - ACF, PACF 로 ARIMA 모델 계수, 차수 선택하기 (2) | 2023.05.27 |
|---|---|
| 시계열 데이터 - 파이썬 auto_arima 및 ARIMA 모델 정리 (2) | 2023.02.13 |
| 시계열 데이터 - 코로나19 확진자 수 ARIMA 모델로 예측하기 (1) (0) | 2023.02.08 |
| 시계열 데이터 - 계절성 ARIMA 모델, SARIMA (0) | 2023.02.07 |
| 시계열 데이터 - AR,MA,ARIMA 모델 (2) | 2023.01.21 |



