시계열 데이터 공부를 시작하고 거의 한 달 만에 ARIMA 모델까지 오게 되었다. 그동안 다른 공부할 거리 때문에 너무 바빴는데, 일 하나가 끝나면 다른 일이 생기고 계속 바쁜 나머지 공부에 많은 시간을 투자하지 못 한 것 같아 아쉬운 마음이 든다. 1월이 거의 다 끝나가는데 아쉬운 생각이 든다. 빨리 ARIMA 모델까진 공부를 마치고 실전 공부를 할 예정이다.
각설하고 이번 포스팅에서는 AR,MA 모델을 공부하고 대망의 ARIMA 모델까지 공부해보도록 하겠다. 사실 앞선 포스팅들을 쓰면서 내용을 자세하게 공부하다 보니 지금 공부할 ARIMA 모델의 내용들의 베이스는 이미 다 공부한 감이 있어서, 공부하는 데에 그렇게 어려울 것 같지는 않다. ARIMA 모델의 AR 모델부터 시작해서, MA, ARIMA 모델까지 개념을 잡고 마지막에 항상 하던 대로 APPLE의 주식 가격을 토대로 ARIMA 분석을 진행해보도록 하겠다.
들어가기 전
앞에서도 몇 번 사용한 개념인 '다중선형회귀'를 모르는 분들이라면 글을 이해하기가 꽤 어려우실 것 같다. 아무래도 내가 공부하면서 배운 내용들을 기록하듯이 포스팅을 작성하고 있어서 내 기준에서 이미 알고 있는 내용들은 설명을 많이 생략했다.
헷갈리기 쉬운 부분을 하나만 짚고 넘어가고 싶다. 자주 등장할 기호 y는 실제 데이터값과 예측값 두 가지 의미가 섞여서 사용된다. 이는 y 의 시점에 따라 달라진다. 예를 들어 시점이 t 까지만 있는 데이터라면, y(t+1)은 자연스럽게 예측값이, y(t)는 실제 데이터 값이 된다. 자주 등장하는 ε 또한 시점에 따라 백색소음, 혹은 오차를 의미할 수 있다. 이는 잔차라는 용어로도 사용된다.
AR모델 (AutoRegressive Model)
일반적인 다중선형회귀 모델들은 그 데이터에 영향을 끼치는 여러 요인들을 변수로 삼아 값을 예측하고자 한다. 예를 들면 이런 식이다. y라는 데이터를 예측하기 위해 요인들(x)이 p개 사용된 모습이다. 그리고 그 요인들 앞에 가중치 β가 붙는다.

자기회귀모델 AR 모델은, 이 요인들이 다른 것이 아닌 자기 자신의 데이터이다. 바로 이런 식이다.

앞의 c가 추가된 것, β가 Φ로 바뀐 것을 제외하면 완전히 똑같음을 확인할 수 있다. 중요한 것은 c도 Φ처럼 데이터를 기반으로 추정해야 하는 변수라는 것이다.
여기서 ε은 백색소음을 의미한다고 한다. 어떤 자료에 White Noise를 평균이 0, 분산이 1인 정규분포에서 랜덤으로 추출한 값이라고 하는데, 내가 생각하기로 중요한 것은 평균이 0이고 분산이 일정하다는 점이고 분산이 꼭 1이어야 하는 것은 아니다. 선형회귀모형은 데이터를 가장 좋게 추정하는 직선이라서 데이터가 흐트러져 있어 좋은 선형회귀모형을 만들기 어렵다면 오차의 분산은 커질 수밖에 없다.
다시 본론으로 돌아가면 어느 시점까지의 데이터를 사용할 것이냐에 따라 p가 결정된다. 예를 들어 시점 t를 기준으로 t-2까지의 데이터로 추정하려고 하면 AR(2) 모델이 될 것이다.
AR 모델을 포함해서 MA, ARIMA 모델에서 차수를 결정하는 과정은 분석가에게 달렸다. R같은 프로그램에선 자동적으로 정해주는 과정이 있는 것 같지만 현재는 파이썬으로 분석을 진행하고 있으므로, 데이터를 보고 차수를 결정해주어야 한다. 차수를 결정하는 방법은 ARIMA 모델에서 한 번에 소개하는 것이 좋을 것 같다.
내 블로그에서 항상 사용하는, 비정상성을 띄는 APPLE 주식 가격 데이터로 코드를 한 번 짜보았다.
statsmodes 패키지에 이미 좋은 함수들이 다 들어있는 것으로 보여서 그대로 사용하기로 했다. AutoReg 함수는 MLE (Most Likelihood Estimate)를 사용하여 적절한 계수들을 다 찾아준다고 한다. 이는 선형회귀에서 사용하는 방식인데, 데이터들을 갖고 분산과 평균을 복잡하게 조합하다 보면 구할 수 있게 된다. 중요한 포인트는 우리가 직접 할 필요 없이 컴퓨터가 알아서 해준다는 점이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
import pandas as pd
from statsmodels.tsa.ar_model import AutoReg
import matplotlib.pyplot as plt
# Load the stock price data for Apple Inc.
df = pd.read_csv('https://www.alphavantage.co/query?function=TIME_SERIES_DAILY_ADJUSTED&symbol=AAPL&apikey=R1A10JZ8TS3877SK&datatype=csv&start_date=2010-01-01')
# Fit an AR model to the closing price
closing_price = df["close"]
model = AutoReg(closing_price, lags=1)
model_fit = model.fit()
# Get the predictions
predictions = model_fit.predict(start=len(closing_price), end=len(closing_price)+100)
# Plot the original data
plt.plot(closing_price, label='Original Data')
# Plot the predictions
plt.plot(predictions, label='AR(1) Predictions', linestyle='--')
# Add labels and legend
plt.xlabel('Time')
plt.ylabel('Closing Price')
plt.legend()
# Show the plot
plt.show()
|
cs |

그렇다면 그나마 정상성을 띄는 1차 차분 데이터로 한 번 진행해보도록 하겠다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
df['diff'] = df['close'].diff()
df = df.dropna(subset=['diff'])
diff_price=df['diff']
model = AutoReg(diff_price, lags=3)
model_fit = model.fit()
# Get the predictions
predictions = model_fit.predict(start=len(diff_price), end=len(diff_price)+100)
# Plot the original data
plt.plot(diff_price, label='Original Data')
# Plot the predictions
plt.plot(predictions, label='AR(1) Predictions', linestyle='--')
# Add labels and legend
plt.xlabel('Time')
plt.ylabel('Diff Price')
plt.legend()
# Show the plot
plt.show()
|
cs |

야심차게 코드를 돌려봤는데 좋지 못한 결과가 나왔다. 아래와 같은 오류가 뜨는데 이것과 연관이 있는 것인지, 아니면 AR 모델이 원래 이런 것인지 고민을 했었다.

AR(2), AR(3) 등으로 많이 돌려봤는데도 같은 현상만 일어났다. 그래서 아래 코드를 통해 Φ(1)을 확인해보고자 했다.
|
1
2
|
coef = model_fit.params
print(coef)
|
cs |
그 결과 다음과 같은 결과가 나왔다.

이 자료를 통해 얻은 결론은, 차분 데이터는 White Noise에 가까운 정상성 데이터이기 때문에, AR 모델로 예측하는 것이 별 의미가 없다는 것이다. 왜냐하면 White Noise의 정의가 자기상관이 없는 데이터인데, 이걸 자기상관이 있다고 생각하여 분석하는 AR 모델로 분석하려 했으니 좋은 결과가 나올리가 없었다. AR 모델로 좋은 결과를 얻으려면 White Noise는 아니지만 정상성을 적당히 갖는 데이터를 사용하는 것이 좋을 것 같다. (최소한 r(1)이 높은 가격을 갖긴 해야 AR(1)에서 Φ(1)이 의미있는 값을 갖는다.) 찾아본 바 ARIMA 모델에서도 AR(p) 에서 p를 0으로 선택하는 경우도 많은데, 이는 ARIMA 모델을 다룰 때 더 자세히 설명해보도록 하고 넘어가고 싶다. (ACF, PACF 를 보고 AR 모델의 차수를 결정하는데, APPLE 주식 가겨의 PACF, ACF를 미리 본 결과 차수를 0으로 결정하는 것이 맞는 것 같다. 이는 뒤에서 더 자세히 다루어 보겠다.)
한 줄 정리 : 정상성 데이터여도, 데이터에 따라 AR 모델을 적용해도 좋은 결과가 나오지 않을 수도 있다.
코드는 삭제해버릴까 하다가 쏟은 시간이 아깝기도 하고 나같은 뻘짓을 하는 분이 없길 바라며 그대로 남겨둔다.
추가로 AR(1) 모델 중 c, Φ 의 값에 따라 백색소음, 확률보행 등으로 분류하기도 하고, AR(1) 모델이 정상성을 만족할 조건등을 따지기도 하던데, ADF Test 에서 단위근을 설명할 때와 논리구조가 똑같아서 생략하기로 한다. (단순선형회귀로 설명했다.)
https://tiabet0929.tistory.com/5
시계열 데이터 - 정상성 분석하기, ADF test
ARIMA 모델을 분석하기 전, 파이썬을 이용해 정상성을 검증해보는 시간이 필요할 것 같다. 사실 이번에 정상성에 대해서 추가로 공부하면서, 새롭게 깨달은 사실이 더 있었다. 바로 정상성 데이터
tiabet0929.tistory.com
MA모델 (Moving Average Model)
MA 모델도 다중선형회귀와 닮아있다. 아래 수식은 MA(q) 모델이다.
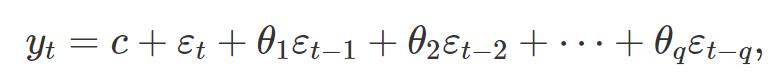
여기서 c는 데이터들의 평균을 의미한다.
즉, MA 모델의 핵심은 이전 데이터들의 오차들을 요인으로 사용하여 적절한 회귀선을 생성하는 것이다. 평균에다가 오차들을 사용해 보정을 하면 대강 미래 데이터를 예측할 수 있을 것이다. 수식적으로는 이렇게 오차로 이해할 수 있지만, 좀 더 개념적으로 접근해본다면, MA 모델은 과거의 충격들의 선형결합으로 한 변수를 설명하는 것이다. 예를 들어보면, 큰 변화 없이 잔잔히 흘러가는 주식 그래프가 있다고 가정했을 때, 어느 날 갑자기 상한가를 치고 주식이 크게 상승한 것이다.

이런 상승을 '충격'이라고 표현한다. 충격은 오차를 만든다. 이 날 주식이 크게 상승하면 다음 날에는, '전날 크게 상승했으니 오늘도 상승할 것이다' 혹은, '오늘은 하락할 것이다' 처럼 전날의 영향을 의식하지 않을 수 없다. 이러한 영향이 얼마나 오래 가는지를 파악하여 MA 모델에 사용하면 되는 것 같다.
MA 모델은 우리말로는 이동평균선 정도가 되는데, 주식 공부를 할 때 거의 맨 처음 배울 정도로 기초적인 지표 중 하나가 바로 이동평균선이다. 그래서 나는 이 이동평균선이 그 이동평균선인 줄 알고, 60일선, 120일선 같은 선이 사실은 60일 동안의 가격 평균이 아니라 이런 MA 모델인 줄 알았다. 그런데 MA 모델은 예측모델이지만 주식의 이동평균선은 기록들로 만들어진 일종의 지표이다. 이상해서 찾아봤더니, 역시 주식의 이동평균선은 단순히 '기간 동안 가격의 평균'에 불과했다.
AR 모델과 MA 모델을 자세히 다루면서, 하나 깨달은 점은 무조건 데이터가 정상성을 띄어야 한다는 것이다. AR과 MA 모델 모두 근본적으로는 선형회귀 모델이다. 선형회귀 모델에선 평균과 분산이 일정한, 즉 정상성을 띄는 데이터가 굉장히 중요하다. 비정상적인 데이터를 그대로 적용하면 이전의 데이터들에서 유의미한 평균과 분산을 얻을 수가 없기 때문에 모델을 예측하기가 힘들다.
한 줄 정리 : AR과 MA 모델은 선형회귀 모델 -> 선형회귀 모델은 평균과 분산을 사용해서 만들어지는 모델 -> 평균과 분산이 시점에 따라 일정하지 않다면 (데이터가 비정상적이라면) 모델의 결과가 매우 나쁨 !
아무래도 그냥 넘어가기 심심하니 AR 모델에서와 마찬가지로 MA 모델로 한 번 예측해보려 했는데, 찾아보니 MA 함수는 존재하지 않아서 바로 ARIMA 모델로 넘어가기로 하겠다.
AR 모델과 MA 모델은 결국 자기 자신의 과거 데이터들로 자신을 설명하고자 하는 점이 닮았다. 그래서 AR 모델과 MA 모델은 상호변환이 가능하다고 하는데, 자세히 보고 넘어가지는 않겠다.
ARIMA 모델 (AutoRegressive Integrated Moving Average Model)
이제 대망의 ARIMA 모델 차례이다.
ARIMA 모델은 이름에서도 살짝 알 수 있지만, AR 모델과 MA 모델의 결합이다. 그런데 그냥 결합한 것이 아니고 Integrated 하여 결합된 모델이다. Integrated 는 번역하자면 '누적' 정도의 의미를 갖는데, Differenced의 역순의 의미이다.

ARIMA 모델을 수식으로 표현하면 위와 같다. 정말로 AR 모델과 MA 모델의 수식을 합쳐놓은 모습이다. 하나 달라진 건 y에 프라임 기호 ( ' ) 가 붙어있다는 점이다. 이는 차분이 몇 번 되었는지를 의미하는 기호다. 즉 ( " ) 이 붙어있으면 2차 차분을 진행한 것이다. 얼핏 보면 굉장히 복잡해 보이는 수식이지만, 선형회귀와 AR, MA 에 대해 잘 알고 있다면 간단명료해 보인다.
한마디로 정리하면 ARIMA 모델은, (필요하다면 차분을 진행한 - I) 이전 데이터 값들 (AR)과 오차 값들(MA)을 이용한 다중선형회귀 모델인 것이다. 이때 AR 모델의 차수를 p, MA 모델의 차수를 q, 차분의 횟수 d를 사용해, ARIMA(p,d,q) 모델이 탄생하는 것이다.

표류를 포함하는 확률보행이란, 상수 c가 0이 아닌 경우에서 발생하는데, c가 0이 아니므로 어떠한 추세가 존재하게 된다.
c가 0보다 크면 상승추세, 작으면 하락추세가 보일 것이다.
Otexts에선 예시를 보여줄 때 R을 사용하는데, R의 Auto ARIMA 함수는 p,d,q를 알아서 적절하게 찾아준다. 하지만 파이썬에는 이런 기능이 없다. 그래서 적절한 p, d, q 를 찾는 방법을 알아보고자 한다.
이 영역은 순전히 데이터 분석가의 몫이다. 그리고 아래에 소개할 차수 결정법도 하나의 방법론을 제시할 뿐, 절대적으로 이것이 옳다! 이런 느낌은 아니다. 시간이 여유롭다면 차수를 바꿔가면서 여러 모델을 시도해보는 것도 좋은 방법일 것 같다.
1. 차분 차수 d 결정법
Otexts에 따르면 웬만해선 2차 차분 이상으로 진행하는 일은 일어나지 않는다고 한다. 이 문장을 토대로 데이터가 비정상적이라면 1차 차분, 1차 차분을 해봐도 평균이 일정하지 않는 추세를 보인다면 2차 차분까지 진행하면 될 것 같다. (데이터를 정상적으로 만드는 것이 ARIMA 모델의 중요한 과제이다.)
데이터의 정상성을 판단하는 과정은 ADF Test나 ACF 등이 있지만 그래프를 보고 판단하는 방법이 제일 빠를 것 같다.
2. AR 모델과 MA 모델의 차수 p, q 결정법
AR 모델과 MA 모델의 차수는 ACF와 PACF의 그래프를 보고 판단한다.
보기 쉽게 테이블로 소개한다.
| ACF | PACF | |
| AR(p) | 그래프가 서서히 감소 or 사인 함수 모양 | 그래프가 p lag 이후로 절단 |
| MA(q) | 그래프가 q lag 이후로 절단 | 그래프가 서서히 감소 or 사인 함수 모양 |
사인 함수 모양 : 0을 기준으로 위아래로 튀는 그래프를 의미한다.
절단 : 그래프가 갑자기 뚝 떨어질 경우를 의미한다. ex) 0.9 --> 0.1
어째서 이렇게 판단하는지는 AR 모델과 MA 모델, ACF와 PACF의 의미를 깊이 생각해봐야 할 것이다.
간단히 짚고 넘어가면 ACF는 시차 간의 상관관계를, PACF는 시차 사이의 영향을 제거하고 순전히 그 시차의 상관관계를 의미한다.
AR 모델의 차수 먼저 이해해보자.
AR 모델은 과거의 데이터값들로 현재의 데이터를 추정하는 모델이다. T의 데이터를 AR(3)으로 예측한다고 하면 T-1, T-2, T-3의 데이터만 선형회귀모델의 요인으로 채택하는 것이다. 즉, AR 모델은 T-1, T-2, T-3 그 당시의 데이터만 중요할 뿐, 그들끼리 얼마나 상관이 있는지는 중요하지 않다. 그래서 ACF의 그래프가 서서히 감소하거나 사인 함수 모양이면 무시하고, PACF에서 현재 시점 T와 상관이 있는 데이터들만 쏙쏙 뽑아서 사용하게 되는 것이다.
MA 모델의 차수도 비슷하다.
MA 모델을 설명할 때 과거의 충격들의 선형결합이라고 표현했다. 충격은 발생하고 곧바로 사라지지 않고 쭉 남아서 이후 오랜 시간 동안 영향을 미칠 수 있다. 즉, PACF보단 ACF가 더 중요한 의미로 받아들여지는 것이다. 그래프가 q lag 이후로 절단됐다면, q 이전엔 그 충격의 영향 하에 있었다는 의미가 되기 때문이다.
이렇게 차수를 선택하는 방법도 꼼꼼하게 살펴보았다.
마지막으로 ARIMA 모델로 APPLE의 주식 데이터를 직접 돌려보도록 하겠다.
함수는 간단하니까 차수 먼저 선택해보겠다.


일전에 만들어놓은 그래프다. 애플의 주식 그래프는 비정상성을, 차분 데이터는 정상성을 띄고 있음을 ADF Test로 확인한 바가 있었다. 사실 차분 데이터가 완벽히 정상성을 띈다고 말할 수는 없지만, 그래도 우선 1차 차분 데이터를 사용하기로 했다. 따라서 d는 1을 선택해보기로 했다.


역시 이전에 ACF와 PACF 포스팅을 할 때 미리 구해놓은 차분 데이터의 ACF와 PACF이다. ACF는 서서히 감소하는 모습을, PACF는 시차 1 이후로 절단되는 모습을 보인다. 따라서 p = 0, q = 1을 선택하기로 했다.
야심차게 코드를 돌려보았다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
import pandas as pd
from statsmodels.tsa.ar_model import AutoReg
import matplotlib.pyplot as plt
# Load the stock price data for Apple Inc.
df = pd.read_csv('https://www.alphavantage.co/query?function=TIME_SERIES_DAILY_ADJUSTED&symbol=AAPL&apikey=R1A10JZ8TS3877SK&datatype=csv&start_date=2010-01-01')
from statsmodels.tsa.arima.model import ARIMA
# Fit an ARIMA model to the closing price
model = ARIMA(closing_price, order=(0,1,1))
model_fit = model.fit()
print(model_fit.summary())
# Make predictions
predictions = model_fit.predict(start=1, end=len(closing_price)+10)
# Plot the original data and predictions
plt.plot(closing_price, label='Original Data')
plt.plot(predictions, label='Predictions', color='red')
# Add labels and legend
plt.xlabel('Date')
plt.ylabel('Closing Price')
plt.legend()
# Show the plot
plt.show()
# Get the residuals
residuals = model_fit.resid[1:]
# Plot the residuals
plt.plot(residuals, label='Residuals')
# Add labels
plt.xlabel('Date')
plt.ylabel('Residuals')
# Show the plot
plt.show()
|
cs |


야심차게 돌려본 결과는 위와 같았다.
사실 ARIMA (0,1,1) 처럼 돌려버리면 ARIMA 모델의 함수가 y = mx + b 꼴로 일차함수가 나오게 되어, 유의미한 예측을 할 수는 없게 된다. 그래도 예측모델의 그림 (빨간선) 과 잔차를 확인하니 맞게 추정은 된 것 같다.

잔차가 백색잡음을 따르는가는 선형회귀에서 아주 중요한 부분이다. 잔차(실제값 - 예측값)가 일정하지 않다면 좋은 모델이 아니기 때문이다. summary 에서 확인한 정보는 Ljung-Box (Q) 와 Prob (Q) 이다. 이는 잔차 데이터가 정상적인지를 알려주는 자료인데, Ljung-Box 값은 작을수록, Prob 값은 클수록 잔차가 백색소음에 가깝다는 것을 의미한다. 임계치는 0.05인 것으로 생각된다. 아무튼 Ljung-Box 값이 0이 나왔으니 잔차가 랜덤하다는 것이고, ARIMA 모델은 맞다는 것을 의미한다.
AIC, BIC 등이 작을수록 좋은 모델임을 의미한다고도 한다. 단, AIC 나 BIC 는 데이터의 길이가 길수록 크게 나오기 때문에 길이가 다른 모델끼리 비교하는 것은 의미가 없다.
ARIMA 모델의 차수를 여러 번 다르게 해서 시도해본 결과까지 첨부하며 포스팅을 마친다.

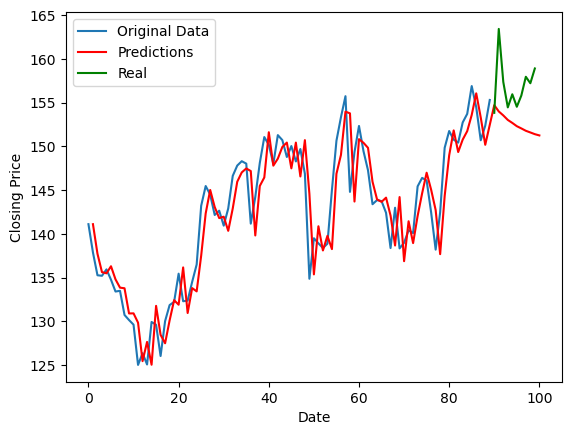

이전 포스팅에서 ARIMA 모델이 그렇게 좋지 못한 모델임을 언급한 바가 있었는데, 과연 그랬다. 아무래도 주식 그래프를 예측하는 것은 외부요인이 워낙 많다보니 시계열 분해를 이용하는 편이 더 좋을 것 같다.
참고자료
https://dong-guri.tistory.com/9
시계열 분석, ARIMA model (Autoregressive Integrated Moving average Model)
들어가기 앞서 . . - 석사 과정 중에 공부하던 시계열 분석에 대해 기억을 더듬으며 정리할 예정이다. 시계열 분석이라는 항목이 수학적으로 정리하기 어렵고, 방법론도 다양해서, 글로 모든 내
dong-guri.tistory.com
https://otexts.com/fppkr/arima.html
Chapter 8 ARIMA 모델 | Forecasting: Principles and Practice
2nd edition
otexts.com
https://assaeunji.github.io/statistics/2021-08-23-arima/
시계열 분석 시리즈 (2): AR / MA / ARIMA 모형, 어디까지 파봤니?
이번 포스팅은 실전 시계열 분석: 통계와 머신러닝을 활용한 예측 기법 책과 Forecasting: Principles and Practice책을 기반으로 AR, MA, ARIMA 모형을 정리하고자 합니다. 제목은 “어디까지 파봤니”로 거
assaeunji.github.io
위키피디아
'시계열 데이터' 카테고리의 다른 글
| 시계열 데이터 - 코로나19 확진자 수 ARIMA 모델로 예측하기 (1) (0) | 2023.02.08 |
|---|---|
| 시계열 데이터 - 계절성 ARIMA 모델, SARIMA (0) | 2023.02.07 |
| 시계열 데이터 - 자기상관함수 ACF와 PACF (2) | 2023.01.15 |
| 시계열 데이터 분석 이론 정리 - 정상성과 비정상성 (0) | 2023.01.09 |
| 시계열 데이터 - 정상성 분석하기, ADF test (0) | 2023.01.02 |



