인공지능 강의를 듣다 보면 항상 나오는 개념이 몇 개 있다. 그 중 하나가 EM 알고리즘이다. 처음에 이 알고리즘에 대해 수업을 들을 때는 뭔 말인지 감도 안오고 어려운 느낌이 있었다. 하지만 내용을 알고 보면 그렇게까지 어려운 건 아니라, 차근차근 정리해보고자 한다.
EM알고리즘의 목적은 MLE
EM알고리즘을 먼저 언제 사용하는 지를 정확하게 아는 것이 이해가 쉬울 것 같다.
그러기 위해선 설명해야 하는 개념이 있는데 우도함수다. 우도함수는 어떤 데이터의 분포(이항분포인지, 다항분포인지 확률분포의 종류를 의미)를 알고 있지만 정확한 모수(이항분포에서 특정 사건이 일어날 확률)를 알지 못할 때, 이 정확한 모수, 즉 파라미터를 찾기 위해 사용된다. 일반적으로 확률분포에서 모수라 함은 평균, 표준편차 같은 데이터의 특징을 나타낼 수 있는 수를 말한다. 우도함수를 구하는 방법은 간단하다. 모든 데이터를 분포의 확률밀도함수에 대입한뒤, 전부 곱해주면 된다. 데이터가 정규분포를 따른다고 가정한 상태라면, 우도함수를 수식으로 나타내면 아래와 같다.


즉, 우도함수는 확률밀도함수 식의 $x$ 자리에 모든 데이터를 집어넣어 곱하여 구할 수 있다. 이를 모든 확률분포에 일반화하면 다음과 같은 식으로 표현된다.

그리고 이 우도함수의 값을 최대화시키는 지점이 바로 최적의 $\theta$, 즉 최적의 모수가 되는 것이다. 그리고 이 우도함수를 최대화하는 과정을 MLE, Maximum Likelihood Estimation라고 부른다. 대부분의 경우에서 MLE는 우도함수에 로그를 씌운 다음 편미분을 통해 구할 수 있다. 로그를 씌우는 것은 함수의 곱셈에 로그를 씌우면 덧셈으로 변환되는 성질을 이용, 계산을 편리하게 하는 것이다. 정규분포의 예시에서 평균을 알고 싶다면, 우도함수에 로그를 씌운 것을 평균에 대해 편미분하면 된다.


이런 식으로 극값의 성질을 이용한다면 손쉽게 MLE를 수행할 수 있다. 이렇게 보면 모든 경우에서 편미분을 통해 MLE를 수행할 수 있을 것 같지만, 항상 예외가 존재한다.
EM 알고리즘을 사용해야 할 때
EM 알고리즘을 사용해야 하는 경우는 편미분을 통해 직접 MLE를 구할 수 없는 경우다. 그런 경우는 결측값이 있는 데이터가 있거나, 데이터가 한 분포에서 나온 것이 아닌, 평균과 표준편차가 다른 여러 개의 확률분포에서 관측된 후 다 섞여 있을 때 (이 상황은 머신러닝에서 클러스터링과 유사한 상황) 같은 경우다. 이런 상황을 잠재 변수, Latent Variable이 존재할 때라고 정의한다. 데이터에 결측치가 있는 경우라면, 모든 데이터의 값을 알고 있어야만 가능한 편미분을 통한 MLE는 불가능하게 된다. 또한, 동일한 확률분포에서 독립적으로 관측된 데이터라는 가정이 깨져도 역시 편미분을 통해서는 MLE를 구할 수 없다.
EM 알고리즘 과정
그러면 이젠 EM 알고리즘의 과정에 대해서 간단하게 정리해보고자 한다. 워낙 다른 글들도 정리를 잘 해놓아서 나는 간단하게만 정리하려고 한다.
EM 알고리즘은 이름에서도 알 수 있듯이 0. 잠재 변수와 모수 초기화 (랜덤하게) 1. 잠재 변수의 기댓값 계산 (Expectation) 2. 모델의 모수 최대화 (Maximazation) 3. 잠재변수의 기댓값, 모델의 모수가 수렴할 때까지 반복 으로 이루어진다.
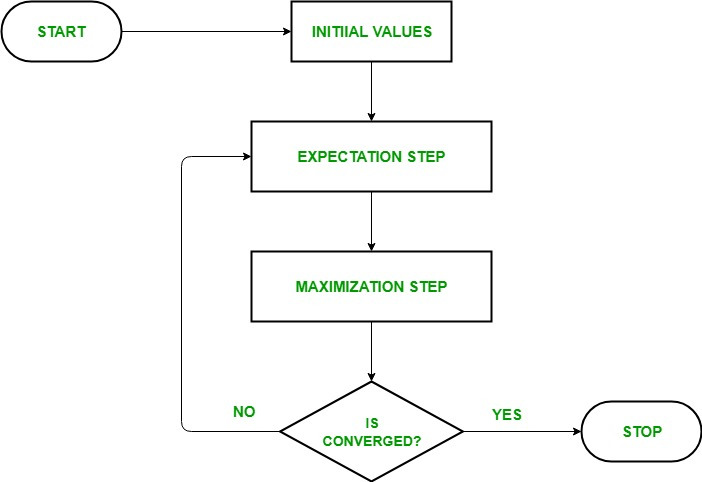
알고리즘 구성 자체는 꽤 간단하다. M 단계에서 추정된 모수는 다시 E 단계로 넘어가서 재사용되고, E 단계에서 추정된 모수를 통해 잠재 변수의 기댓값을 다시 계산하는 재귀적인 성격을 띄고 있다.
EM 알고리즘 예시
오래됐고 유명한 알고리즘이다 보니 다른 곳들에서도 좋은 예시가 많다.
여기 한 교수님이 쉽게 예시로 정리해주신 영상도 존재하고
EM 알고리즘 예시로 쉽게 이해하기 (Expectation maximization, EM algorithm)
기댓값 최대화 알고리즘(expectation-maximization algorithm, EM algorithm)은 모수에 관한 추정 값으로 로그 가능도(log likelihood)의 기댓값을 계산하는 기댓값 (E) 단계와 이 기댓값을 최대화하는 모수 추정값
modern-manual.tistory.com
가장 흔한 동전 던지기 예시에서도 정리된 바가 존재한다. 나도 따로 공부를 정말 많이 했는데, 굳이 또 일일이 정리할 필요까진 없을 것 같아서 여기선 ChatGPT의 설명으로 대신하고자 한다. 문제 상황은 혼합 가우시안 모델이다. 어려울 건 없고 위에서 잠깐 말했듯 서로 다른 정규분포들에서 관측된 데이터가 뒤섞인 상황에서 각 정규분포의 모수를 추정하는 상황이다.



책임도라는 단어가 혼동이 되기도 하는데, 그냥 확률 혹은 기대값이라고 생각하면 편하다.

지금은 처음부터 너무 값이 수렴해버렸다. (기대값이 양쪽이 너무 차이가남)

아무튼 이렇게 M 단계에서 평균과 분산 같은 파라미터를 다시 업데이트하게 된다. 이후 단계를 반복하면서, 파라미터 업데이트가 잘 일어나지 않는 수렴상태에 다다르면 알고리즘은 끝난다.
예시를 보면 알겠지만, EM 알고리즘은 잠재 변수가 있는 영역에서 폭넓게 활용될 수 있다. 결측치가 있는 경우에 결측치 추정과 모수 추정을 동시에 할 수 있고, 클러스터링과 문서의 토픽 모델링(LDA), 나아가 이미지 복원에도 사용된다고 한다.
'통계학' 카테고리의 다른 글
| 통계학 - 독립변수의 개수가 늘어날수록 결정계수가 증가하는 이유 (2) | 2023.11.25 |
|---|
