오늘은 ARIMA 모델로 넘어가기 전, 시계열 데이터의 중요 개념들을 다시 한 번 정리하고
시계열 데이터 분석을 할 때 가장 기초로 여겨지는 차분, differencing에 대해 공부해보려고 한다.
앞서 공부한 바로는 시계열 데이터의 3요소인 주기(Cycle), 추세(Trend), 계절성(Seasonality) (오차까지 포함하면 4요소지만 오차는 기본적으로 예측할 수 있는 것이 아니다!) 가 포함되면 비정상성을 띈다고 부른다. 이를 자세히 살펴보고 싶다.
시계열 데이터 공부에 아주 큰 도움을 주고 있는 온라인 교과서, O-text에 실려 있는 예시이다.

나머지는 제쳐두고, 내가 주목하고 싶은 것은 b와 g 이다.
우선 b이다. 구글 주식 가격의 200일 동안의 가격 변동을 나타낸 그래프이다. 160일 쯤에 데이터가 평균을 크게 벗어난 사실을 누구나 알 수 있다. 그렇다면 이는 정상성을 나타내는 시계열 데이터이다. 이전 포스팅에서도 다루었듯이 축적된 데이터들로 예측할 수 없다면 정상성을 나타내는 시계열이다. 또한, 주기나 계절성, 추세가 보이지 않으므로, 아마 오버슈팅이 일어난 데이터가 없었어도 정상성 데이터로 분류되었을 것 같다.
g는 캐나다 일부 지역에서 포획된 이리의 연간 수이다. 확실히 주기성을 가졌다는 것이 눈에 띈다. 앞선 포스팅에서 주기성만을 가진 데이터는 정상성 데이터로 분류한다고 설명했다. 하지만 이정도면 축적된 데이터들로 미래의 데이터를 충분히 예측 가능한 것처럼 보인다. 주기가 40년 정도로 매우 뚜렷하기 때문이다. 그러나 시계열 데이터에서 주기는 불규칙한 period를 갖는다. 현상을 정확하게 분석해보면, 이리의 개체 수가 매우 늘어나면 이리의 먹이가 줄어들기 때문에, 자연스레 이리가 줄어들고, 이리가 줄어들면 다시 먹이는 늘어나서 또 이리가 늘어나는 구조이다. 이런 배경을 이해하고 나면, 주기가 앞으로도 쭉 40년이라고 할 수 없다. 따라서 주기를 갖는 시계열 데이터를 정상성 데이터로 분류하는 것이다.
이 예시를 공부하다가 한 가지 더 의문이 생겼다. 계절성과 주기에 대해서는 이제 차이도 구분 가능하고 정상성-비정상성으로 구분도 가능한데, 추세에 대해서는 다소 모호한 감이 있었다.
일반적으로 추세를 갖는 데이터란, 장기적으로 증가하거나 감소하는 데이터를 의미한다. 내가 의문을 품은 것은, 증가하고 감소하는 것은 계절성이나 주기성을 갖는 데이터에서도 발견할 수밖에 없는 것이라는 점이었다. 하지만 여기서 중요한 키워드는 "장기적"이었다. 앞선 포스팅에서 계절성과 주기성의 차이를 설명할 때 그 기간과 변화량에 초점을 두었었다. 즉, 계절성을 갖는 데이터들은 1년 내의 시간 내에서 그 변화를 보이기 때문에 추세를 갖는다고 하기 힘들 것이다.
그래서 시계열 분해(Decomposition)를 할 때, '추세-주기 성분', '계절성 성분', '나머지 성분' 이렇게 세 가지 성분을 가지는 것으로 분해한다는 것을 알 수 있었다. 추세-주기 성분은 단순히 추세라고 부르기도 하며, 나머지 성분은 아마도 오차 등을 포함한 성분인 것 같다.
다시 예시로 돌아가보자.

a와 c, e, f는 추세가, d,h는 계절성이 보인다. i는 추세와 계절성 모두 보이는 것처럼 보이고, 또 변동폭이 커지는 것으로 보아 분산도 증가하고 있다. 따라서 이들 데이터는 모두 비정상성 데이터임을 알 수 있다.
다음은 Differencing, 차분이다.
차분에 대해선 간단히 짚고 넘어가면 될 것 같다.

즉, 특정 시간 t에서의 데이터값에서 t-1에서의 데이터값을 뺀 값, 이것이 차분이다. t개의 데이터가 있다면 차분 값은 t-1개의 데이터가 나올 것이다.
차분은 여러 모로 유의하게 쓰일 수 있다.
어떤 수든지 로그를 씌우면 큰 수라도 아주 작은 수치로 전환할 수 있는데, t-1개의 차분값에 모두 로그를 씌워서 그래프로 나타내면 그 값이 아주 작아질 것이다. 1000에 밑이 2인 로그만 씌우더라도 10이 안 되는 작은 수로 전환할 수 있음을 생각해보면 쉬울 것이다. 따라서, 데이터의 추세-주기 성분, 계절 성분을 제거할 수 있다. 이것은 의미가 크다. 비정상적인 데이터를 정상적으로 만들 수 있기 때문이다.
지금까지 공부한 내용을 바탕으로 코딩을 한 번 해 보았다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# Load the stock price data for Apple Inc.
df = pd.read_csv('https://www.alphavantage.co/query?function=TIME_SERIES_DAILY_ADJUSTED&symbol=AAPL&apikey=R1A10JZ8TS3877SK&datatype=csv')
# Convert the 'Date' column to a datetime index
df.index = pd.to_datetime(df['timestamp'])
# Plot the 'Close' column
plt.plot(df['close'])
plt.xlabel('Date')
plt.ylabel('Closing price (USD)')
plt.title('Apple Inc. Stock Price')
plt.show()
# Convert the 'Date' column to a datetime index
df.index = pd.to_datetime(df['timestamp'])
# Calculate the differenced data
df['diff'] = df['close'].diff()
# Plot the differenced data
plt.plot(df['diff'])
plt.xlabel('Date')
plt.ylabel('Differenced data')
plt.title('Apple Inc. Stock Price Differenced Data')
plt.show()
# Calculate the logged data
df['log'] = np.log(abs(df['diff']))
# Plot the logged data
plt.ylim(-10,10) plt.plot(df['log'])
plt.xlabel('Date')
plt.ylabel('Logged data')
plt.title('Apple Inc. Stock Price Logged Data')
plt.show()
|
cs |
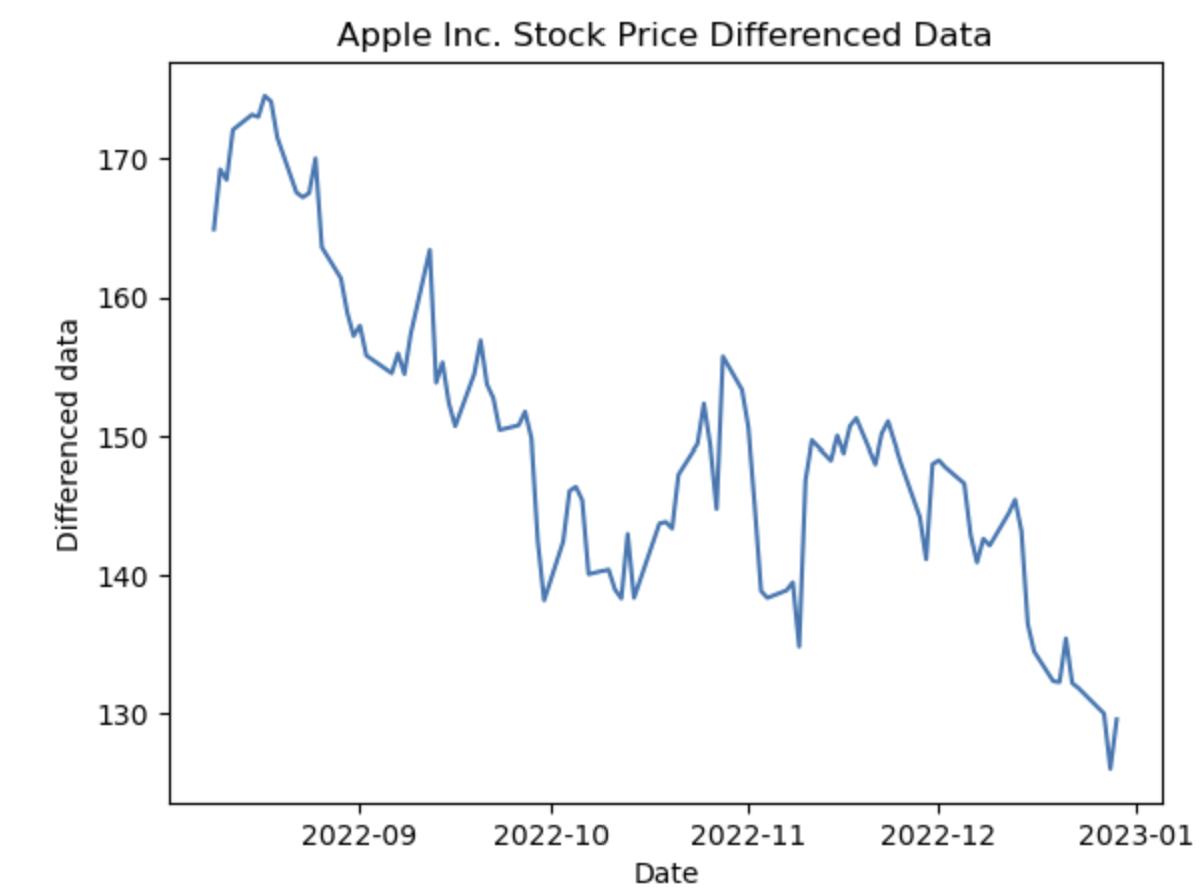
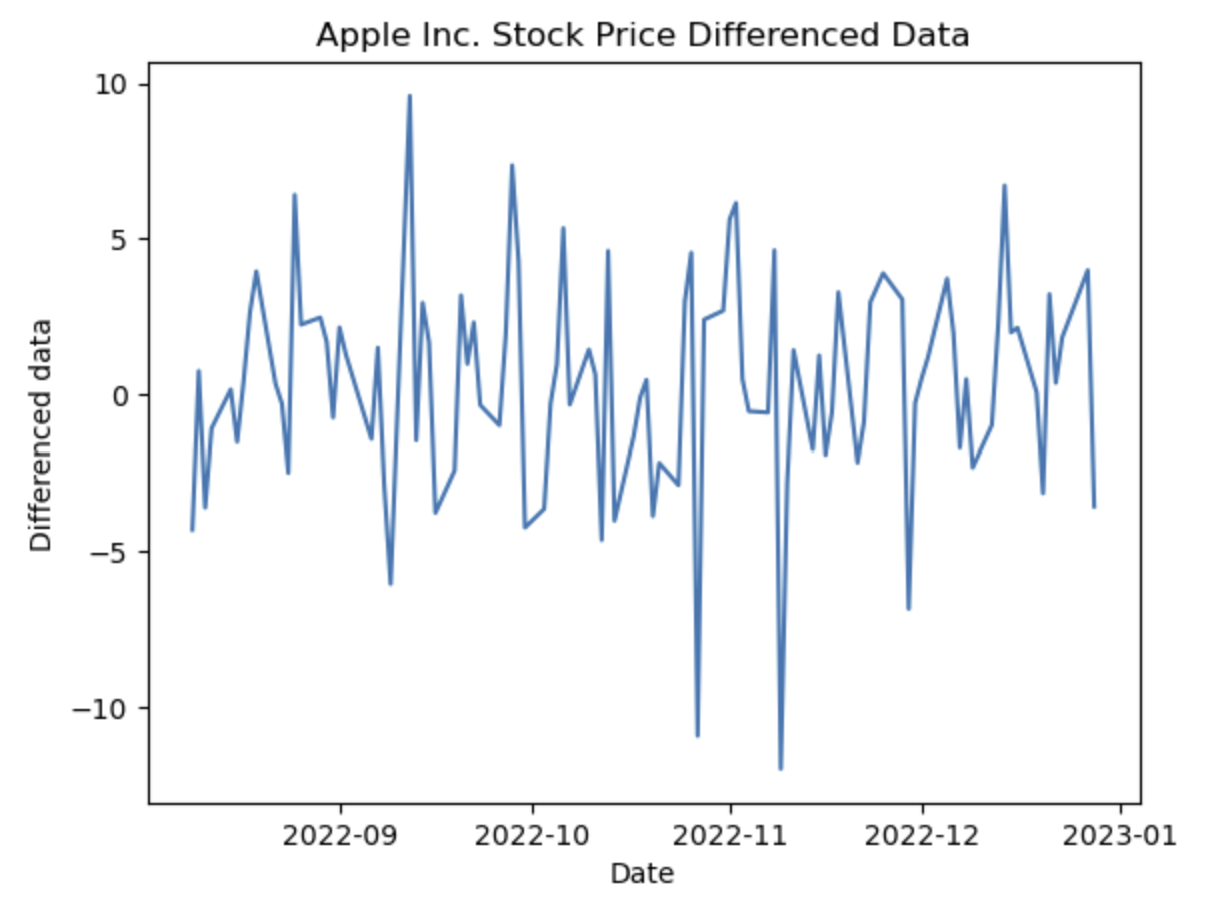
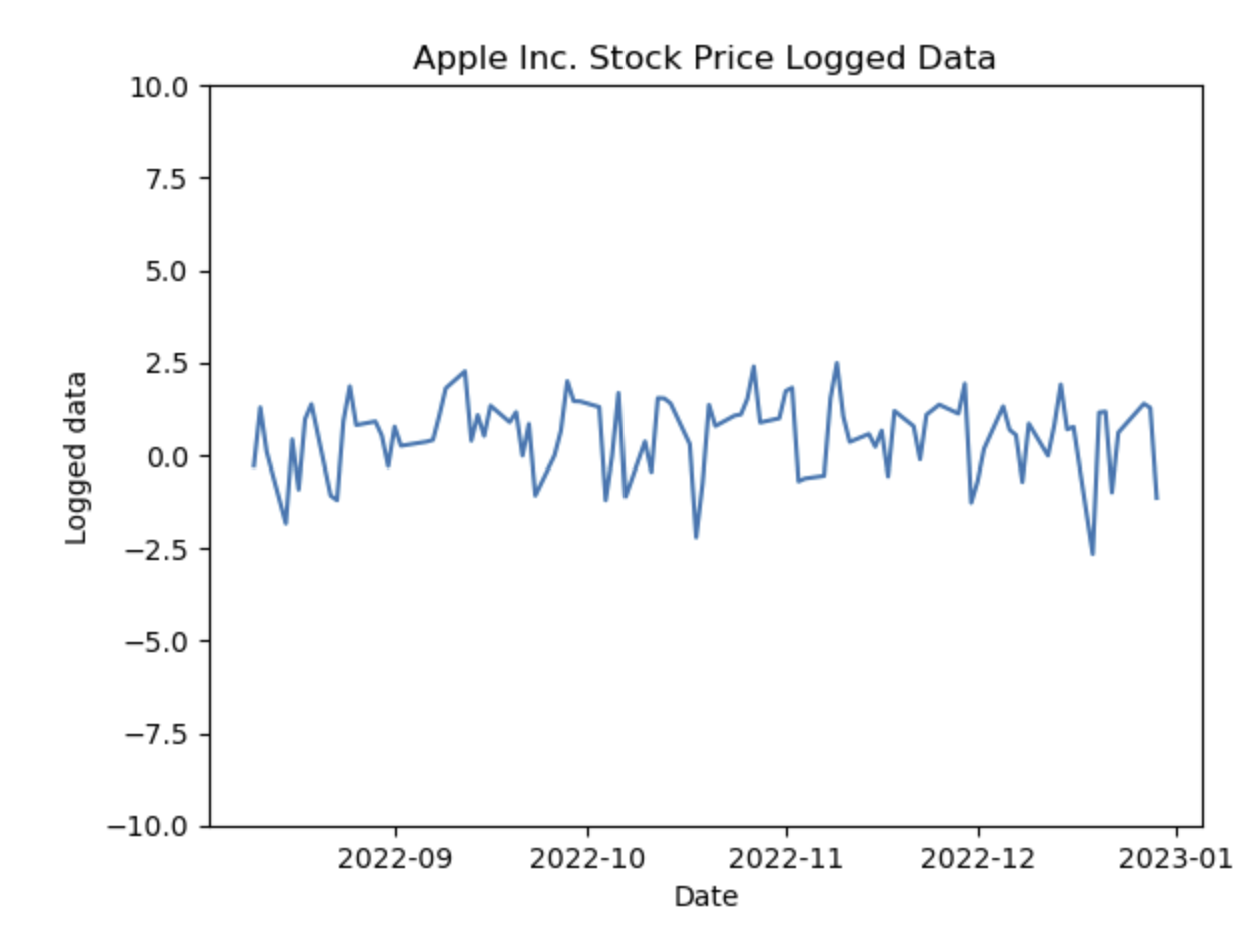
그래프를 그리는 것까진 성공했는데, 아직 섣부르게 추세를 따질 수는 없을 것 같다. 다만 로그를 씌우면 데이터가 다소 정상적인 모습을 띄는 것을 알 수 있다.
이 외에도 2차 차분, 계절성 차분 등 여러 차분이 있지만, 크게 중요하진 않을 것 같아 우선은 제외했다. 나중에 공부하다가 필요하면 추가로 공부해보도록 하겠다.
다음 시간부터는 본격적으로 ARIMA모델을 사용해 시계열 데이터를 분석하는 법을 공부하도록 하겠다.
'시계열 데이터' 카테고리의 다른 글
| 시계열 데이터 - 자기상관함수 ACF와 PACF (2) | 2023.01.15 |
|---|---|
| 시계열 데이터 분석 이론 정리 - 정상성과 비정상성 (0) | 2023.01.09 |
| 시계열 데이터 - 정상성 분석하기, ADF test (0) | 2023.01.02 |
| 시계열 데이터 - 시작 전 (0) | 2022.12.28 |
| 시계열 데이터 - 정상성과 비정상성 (0) | 2022.12.27 |



